我们知道,深度学习最核心的其中一个步骤,就是求导:根据函数(linear + activation function)求weights相对于loss的导数(还是loss相对于weights的导数?)。然后根据得出的导数,相应的修改weights,让loss最小化。
各大深度学习框架Tensorflow,Keras,PyTorch都自带有自动求导功能,不需要我们手动算。
在初步学习PyTorch的时候,看到PyTorch的自动求导过程时,感觉非常的别扭和不直观。我下面举个例子,大家自己感受一下。
>>> import torch >>> >>> a = torch.tensor(2.0, requires_grad=True) >>> b = torch.tensor(3.0, requires_grad=True) >>> c = a + b >>> d = torch.tensor(4.0, requires_grad=True) >>> e = c * d >>> >>> e.backward() # 执行求导 >>> a.grad # a.grad 即导数 d(e)/d(a) 的值 tensor(4.)
这里让人感觉别扭的是,调用 e.backward()执行求导,为什么会更新 a 对象的状态grad?对于习惯了OOP的人来说,这是非常不直观的。因为,在OOP里面,你要改变一个对象的状态,一般的做法是,引用这个对象本身,给它的property显示的赋值(比如 user.age = 18),或者是调用这个对象的方法(user.setAge(18)),让它状态得以改变。
而这里的做法是,调用了一个跟它(a)本身看起来没什么关系的对象(e)的方法,结果改变了它的状态。
每次写代码写到这个地方的时候,我都觉得心里一惊。因此,就一直想一探究竟,看看这内部的关联究竟是怎么样的。
根据上面的代码,我们知道的是,e的结果,是由c和d运算得到的,而c,又是根据a和b相加得到的。现在,执行e的方法,最终改变了a的状态。因此,我们可以猜测e内部可能有某个东西,引用着c,然后呢,c内部又有些东西,引用着a。因此,在运行e的backward()方法时,通过这些引用,先是改变c,在根据c内部的引用,最终改变了a。如果我们的猜测没错的话,那么这些引用关系到底是什么呢?在代码里是怎么提现的呢?
想要知道其中原理,最先想到的办法,自然是去看源代码。
遗憾的是,backward()的实现主要是在C/Cpp层间做的,在Python层面做的事情很少,基本上就是对参数做了一下处理,然后调用native层面的实现。如下:
def backward(tensors, grad_tensors=None, retain_graph=None, create_graph=False, grad_variables=None): r"""Computes the sum of gradients of given tensors w.r.t. graph leaves. ...more comment """ if grad_variables is not None: warnings.warn("'grad_variables' is deprecated. Use 'grad_tensors' instead.") if grad_tensors is None: grad_tensors = grad_variables else: raise RuntimeError("'grad_tensors' and 'grad_variables' (deprecated) " "arguments both passed to backward(). Please only " "use 'grad_tensors'.") tensors = (tensors,) if isinstance(tensors, torch.Tensor) else tuple(tensors) if grad_tensors is None: grad_tensors = [None] * len(tensors) elif isinstance(grad_tensors, torch.Tensor): grad_tensors = [grad_tensors] else: grad_tensors = list(grad_tensors) grad_tensors = _make_grads(tensors, grad_tensors) if retain_graph is None: retain_graph = create_graph Variable._execution_engine.run_backward( tensors, grad_tensors, retain_graph, create_graph, allow_unreachable=True) # allow_unreachable flag
说到Cpp。。。

由于C/Cpp是我的知识盲区,只能通过一顿自行的探索操作,来了解这个执行过程了。
我们先看看e里面有什么。
由于e是一个Tensor变量,我们自然想到去看Tensor这个类的代码,看看里面有哪些成员变量。不幸的是,Python语言声明成员变量的方式跟Java这些静态语言不一样,他们是用到的时候直接用self.xxx随时声明的。不像Java这样,在某一个地方统一声明并做初始化。
当然,我们可以用正则表达式 self\.\w+\s+= 搜索所有类似于 self.xxx = 的地方,于是你会找到一些data, requires_grad, _backward_hooks, retain_grad等等。根据已有的知识,这些看起来都不像。看来相关的成员变量应该在其父类TensorBase里面。不幸的是,TensorBase是用C/Cpp 实现的。这。。。这就又涉及到我的知识盲区了。。。
不过,Python其实还提供了其他的一些方式,来方便我们查看这个对象的属性和状态。那就是vars() 方法和 dir()方法。然而。。。
>>> vars(a) {} >>> >>> >>> >>> dir(a) ['__abs__', '__add__', '__and__', '__array__', '__array_priority__', '__array_wrap__', '__bool__', '__class__', '__deepcopy__', '__delattr__', '__delitem__', '__dict__', '__dir__', '__div__', '__doc__', '__eq__', '__float__', '__floordiv__', '__format__', '__ge__', '__getattribute__', '__getitem__', '__gt__', '__hash__', '__iadd__', '__iand__', '__idiv__', '__ilshift__', '__imul__', '__index__', '__init__', '__init_subclass__', '__int__', '__invert__', '__ior__', '__ipow__', '__irshift__', '__isub__', '__iter__', '__itruediv__', '__ixor__', '__le__', '__len__', '__long__', '__lshift__', '__lt__', '__matmul__', '__mod__', '__module__', '__mul__', '__ne__', '__neg__', '__new__', '__nonzero__', '__or__', '__pow__', '__radd__', '__rdiv__', '__reduce__', '__reduce_ex__', '__repr__', '__reversed__', '__rfloordiv__', '__rmul__', '__rpow__', '__rshift__', '__rsub__', '__rtruediv__', '__setattr__', '__setitem__', '__setstate__', '__sizeof__', '__str__', '__sub__', '__subclasshook__', '__truediv__', '__weakref__', '__xor__', '_backward_hooks', '_base', '_cdata', '_coalesced_', '_dimI', '_dimV', '_grad', '_grad_fn', '_indices', '_make_subclass', '_nnz', '_values', '_version', 'abs', 'abs_', 'acos', 'acos_', 'add', 'add_', 'addbmm', 'addbmm_', 'addcdiv', 'addcdiv_', 'addcmul', 'addcmul_', 'addmm', 'addmm_', 'addmv', 'addmv_', 'addr', 'addr_', 'all', 'allclose', 'any', 'apply_', 'argmax', 'argmin', 'argsort', 'as_strided', 'as_strided_', 'asin', 'asin_', 'atan', 'atan2', 'atan2_', 'atan_', 'backward', 'baddbmm', 'baddbmm_', 'bernoulli', 'bernoulli_', 'bincount', 'bmm', 'btrifact', 'btrifact_with_info', 'btrisolve', 'byte', 'cauchy_', 'ceil', 'ceil_', 'char', 'cholesky', 'chunk', 'clamp', 'clamp_', 'clamp_max', 'clamp_max_', 'clamp_min', 'clamp_min_', 'clone', 'coalesce', 'contiguous', 'copy_', 'cos', 'cos_', 'cosh', 'cosh_', 'cpu', 'cross', 'cuda', 'cumprod', 'cumsum', 'data', 'data_ptr', 'dense_dim', 'det', 'detach', 'detach_', 'device', 'diag', 'diag_embed', 'diagflat', 'diagonal', 'digamma', 'digamma_', 'dim', 'dist', 'div', 'div_', 'dot', 'double', 'dtype', 'eig', 'element_size', 'eq', 'eq_', 'equal', 'erf', 'erf_', 'erfc', 'erfc_', 'erfinv', 'erfinv_', 'exp', 'exp_', 'expand', 'expand_as', 'expm1 ', 'expm1_', 'exponential_', 'fft', 'fill_', 'flatten', 'flip', 'float', 'floor', 'floor_', 'fmod', 'fmod_', 'frac', 'frac_', 'gather', 'ge', 'ge_', 'gels', 'geometric_', 'geqrf', 'ger', 'gesv', 'get_device', 'grad', 'grad_fn', 'gt', 'gt_', 'half', 'hardshrink', 'histc', 'ifft', 'index_add', 'index_add_', 'index_copy', 'index_copy_', 'index_fill', 'index_fill_', 'index_put', 'index_put_', 'index_select', 'indices', 'int', 'inverse', 'irfft', 'is_coalesced', 'is_complex', 'is_contiguous', 'is_cuda', 'is_distributed', 'is_floating_point', 'is_leaf', 'is_nonzero', 'is_pinned', 'is_same_size', 'is_set_to', 'is_shared', 'is_signed', 'is_sparse', 'isclose', 'item', 'kthvalue', 'layout', 'le', 'le_', 'lerp', 'lerp_', 'lgamma', 'lgamma_', 'log', 'log10', 'log10_', 'log1p', 'log1p_', 'log2', 'log2_', 'log_', 'log_normal_', 'log_softmax', 'logdet', 'logsumexp', 'long', 'lt', 'lt_', 'map2_', 'map_', 'masked_fill', 'masked_fill_', 'masked_scatter', 'masked_scatter_', 'masked_select', 'matmul', 'matrix_power', 'max', 'mean', 'median', 'min', 'mm', 'mode', 'mul', 'mul_', 'multinomial', 'mv', 'mvlgamma', 'mvlgamma_', 'name', 'narrow', 'narrow_copy', 'ndimension', 'ne', 'ne_', 'neg', 'neg_', 'nelement', 'new', 'new_empty', 'new_full', 'new_ones', 'new_tensor', 'new_zeros', 'nonzero', 'norm', 'normal_', 'numel', 'numpy', 'orgqr', 'ormqr', 'output_nr', 'permute', 'pin_memory', 'pinverse', 'polygamma', 'polygamma_', 'potrf', 'potri', 'potrs', 'pow', 'pow_', 'prelu', 'prod', 'pstrf', 'put_', 'qr', 'random_', 'reciprocal', 'reciprocal_', 'record_stream', 'register_hook', 'reinforce', 'relu', 'relu_', 'remainder', 'remainder_', 'renorm', 'renorm_', 'repeat', 'requires_grad', 'requires_grad_', 'reshape', 'reshape_as', 'resize', 'resize_', 'resize_as', 'resize_as_', 'retain_grad', 'rfft', 'roll', 'rot90', 'round', 'round_', 'rsqrt', 'rsqrt_', 'scatter', 'scatter_', 'scatter_add', 'scatter_add_', 'select', 'set_', 'shape', 'share_memory_', 'short', 'sigmoid', 'sigmoid_', 'sign', 'sign_', 'sin', 'sin_', 'sinh', 'sinh_', 'size', 'slogdet', 'smm', 'softmax', 'sort', 'sparse_dim', 'sparse_mask', 'sparse_resize_', 'sparse_resize_and_clear_', 'split', 'split_with_sizes', 'sqrt', 'sqrt_', 'squeeze', 'squeeze_', 'sspaddmm', 'std', 'stft', 'storage', 'storage_offset', 'storage_type', 'stride', 'sub', 'sub_', 'sum', 'svd', 'symeig', 't', 't_', 'take', 'tan', 'tan_', 'tanh', 'tanh_', 'to', 'to_dense', 'to_sparse', 'tolist', 'topk', 'trace', 'transpose', 'transpose_', 'tril', 'tril_', 'triu', 'triu_', 'trtrs', 'trunc', 'trunc_', 'type', 'type_as', 'unbind', 'unfold', 'uniform_', 'unique', 'unsqueeze', 'unsqueeze_', 'values', 'var', 'view', 'view_as', 'where', 'zero_'] >>>
可以看到,使用vars()方法,返回的集合是空的。而使用dir(),返回的却又太多了,你都不知道哪些是有用的哪些是没用的,哪些又是我们真正关心的。
怎么办呢?
看来只能Google了。经过一顿调查和连猜带蒙,我得出了一些结论。也不知道是否正确(准确),如果有错误或不准确的地方,还希望有大神不吝指出。
为了解释他们之间的关系,我们先从一个最简单的例子开始。
>>> a = torch.tensor(2.0, requires_grad=True) >>> b = torch.tensor(3.0, requires_grad=True) >>> c = a + b >>> >>> c.backward() >>> a.grad tensor(1.) >>> b.grad tensor(1.) >>>
我们的问题是,c和a是怎么串联起来的?为什么执行c.backward(),会更新a的状态(a.grad的值)?
其实,我们要找的东西,远在天边,近在眼前。
>>> c
tensor(5., grad_fn=<AddBackward0>)
>>>
可以看到,c里面有一个gran_fn变量。这个东西是什么呢?
>>> c.grad_fn <AddBackward0 object at 0x10e56d160> >>> type(c.grad_fn) <class 'AddBackward0'> >>>
可见,这是一个AddBackward0这个类的对象。遗憾的是,这个类也是用Cpp来写的。不过,这不代表我们不能在Python层做一些简单的探索,看看里面有些什么东西。
>>> dir(c.grad_fn) ['__call__', '__class__', '__delattr__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '_register_hook_dict', 'metadata', 'name', 'next_functions', 'register_hook', 'requires_grad']
除去那些特殊方法(以__开头和结束的)和私有方法(以_开头的),范围缩小到['metadata', 'name', 'next_functions', 'register_hook', 'requires_grad’] 这其中,看名字,最可疑的是这个next_functions。我们看看是什么:
>>> c.grad_fn.next_functions ((<AccumulateGrad object at 0x10e56d160>, 0), (<AccumulateGrad object at 0x1205b29b0>, 0)) >>>
看起来,这个next_functions 是一个tuple of tuple of AccumulateGrad and int。
继续探索这个 AccumulateGrad。
>>> ag = c.grad_fn.next_functions[0][0] >>> dir(ag) ['__call__', '__class__', '__delattr__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '_register_hook_dict', 'metadata', 'name', 'next_functions', 'register_hook', 'requires_grad', 'variable']
同样的,去掉那些特殊函数。我们感兴趣的范围缩小到 ['metadata', 'name', 'next_functions', 'register_hook', 'requires_grad', 'variable'] 这其中,除了前面提高过的 'next_functions' 之外,我们惊讶的发现,还有一个 叫 variable 的属性。我们分别都看一下:
>>> ag.next_functions () >>> ag.variable tensor(2., requires_grad=True) >>>
可见,ag1的variable这个属性是一个
tensor(2., requires_grad=True)
这个看起来似乎跟我们前面定义的a是同一个啊。是吗?我们确认一下:
>>> id(a) 4842774104 >>> id(ag.variable) 4842774104 >>>
果然是!
到这里,谜底基本上就呼之欲出了。
当我们执行c.backward()的时候。这个操作将调用c里面的grad_fn这个属性,执行求导的操作。这个操作将遍历grad_fn的next_functions,然后分别取出里面的function(AccumulateGrad),执行求导操作。计算出结果以后,将结果保存到他们对应的variable 这个变量所引用的对象(a和b)的 grad这个属性里面。
于是,当我们执行完c.backward()之后,a和b里面的grad值就得到了更新。
再回到我们开篇提到的稍微复杂点的例子:
>>> import torch >>> >>> a = torch.tensor(2.0, requires_grad=True) >>> b = torch.tensor(3.0, requires_grad=True) >>> c = a + b >>> d = torch.tensor(4.0, requires_grad=True) >>> e = c * d >>> >>> e.backward() >>> a.grad tensor(4.) >>> b.grad tensor(4.) >>> c.grad >>> d.grad tensor(5.)
以此类推,e到各个节点a、b、c、d的关联也就很容易理解了。
>>> e tensor(20., grad_fn=<MulBackward0>) >>> e.grad_fn <MulBackward0 object at 0x111cb5470> >>> e.grad_fn.next_functions ((<AddBackward0 object at 0x110501438>, 0), (<AccumulateGrad object at 0x111cb5fd0>, 0))
分别把next_functions中的function取出来看看
>>> ((f1, _), (f2, _)) = e.grad_fn.next_functions >>> f1 <AddBackward0 object at 0x111cb5fd0> >>> f1.variable Traceback (most recent call last): File "<stdin>", line 1, in <module> AttributeError: 'AddBackward0' object has no attribute 'variable' >>> c tensor(5., grad_fn=<AddBackward0>) >>> c.grad_fn <AddBackward0 object at 0x111cb5fd0> >>> f2 <AccumulateGrad object at 0x1103ee4e0> >>> f2.variable tensor(4., requires_grad=True)
可见,e.grad_fn.next_functions中的第一个function f1,就是c.grad_fn。
不过,如果跟着刚刚的思路,你会觉得意外的是,f1是没有variable 变量的。这是因为,c的结果,是由a和b相加的出来的,这样的变量是非“叶变量”。
如果我们把a、b、c、d、e和他们之间的运算过程理解为一棵树。那么,a、b、d都是我们自己“new”出来的,这样的节点叫叶节点。这些叶节点分别有一个AccumulateGrad 类型的function跟它们对应起来。则像c、e这些,不是我们自己直接创建的,而是通过一些运算得出的,就是非叶节点。对于非叶节点来说,默认情况下他们不需要存储导数值(当然,如果需要,也是有办法做到的)。因此,他们的grad_fn,不需要有一个变量variable 引用着他们。
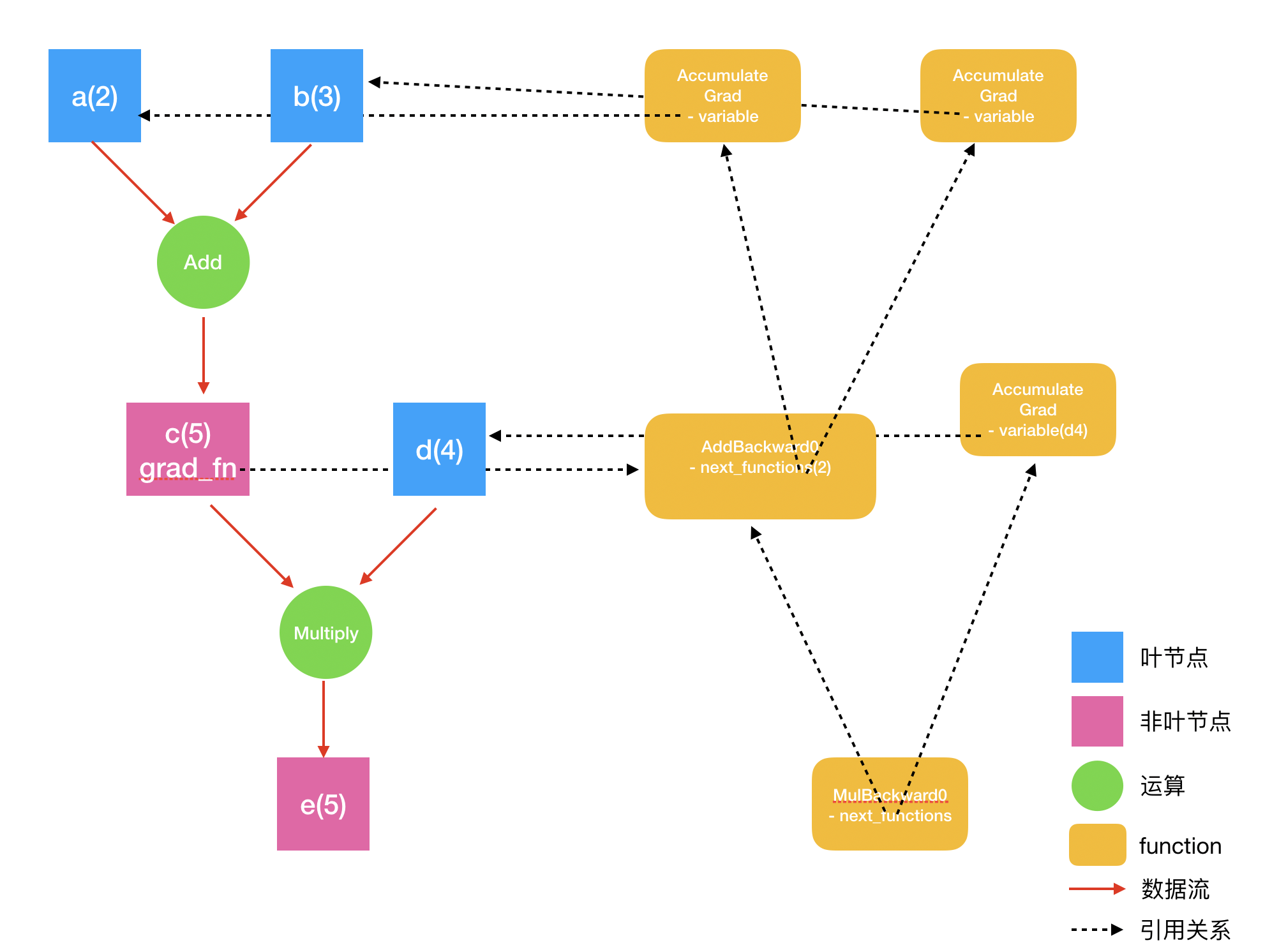
在e.backward()执行求导时,系统遍历e.grad_fn.next_functions,分别执行求导。如果e.grad_fn.next_functions中有哪个是AccumulateGrad,则把结果保存到AccumulateGrad的variable引用的变量中。否则,递归遍历这个function的next_functions,执行求导过程。最终到达所有的叶节点,求导结束。同时,所有的叶节点的grad变量都得到了相应的更新。
他们之间的关系如下图所示:
那么,还有两个问题没有解决:
1. 这些各种function,像AccumulateGrad、AddBackward0、MulBackward0,是怎么产生的?
2. 这些function,比如上面出现过的AddBackward0 、MulBackward0,具体是怎么求导的呢?
对于第一个问题,很自然的猜测,是PyTorch重写了一些操作符,像+,*等。在这个过程中,创建了这些function,并建立起了引用关系。
对于第二个问题,简单的说,就是在每个函数定义的时候,都需要自己定义好forward()和backward()函数。在forward()里面实现这个运算的执行过程。比如,相加、相乘,在backward()则实现这个运算的求导过程。
以上就是我对PyTorch的自动求导原理的理解。只是一个大概的,比较浅显的理解。对于一些更加细节的,包括一些特殊情况的处理,推荐大家看这个视频。讲得非常清楚。
https://www.youtube.com/watch?v=MswxJw-8PvE
参考:
https://pytorch.org/docs/stable/autograd.html#in-place-operations-on-tensors
https://pytorch.org/docs/stable/notes/extending.html
https://www.youtube.com/watch?v=MswxJw-8PvE
写的挺好,感谢(^_^)